Информация
Начав описывать конкретную кибернетическую систему, мы невольно употребляем термин информация, который в своем разговорном, неформальном значении хорошо знаком и понятен каждому культурному человеку. Теперь мы введем кибернетическое понятие информации, имеющее точный количественный смысл.
Представим себе две подсистемы A и B (рис. 1.2), связанные между собой таким образом, что изменение состояния системы A влечет изменение состояния системы B. Это можно выразить такими словами: подсистема A воздействует на подсистему B.
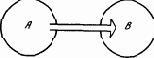
Рис. 1.2. Связанные подсистемы
Рассмотрим подсистемы B в некоторый момент времени t1
и в более поздний момент времени t2. Первое обозначим через S1, второе — через S2. Cостояние S2 зависит от состояния S1. Однако оно не определяется состоянием S1
однозначно, а зависит от него вероятностным образом, ибо мы рассматриваем не идеализированную теоретическую систему, подчиняющуюся детерминистическому закону движения, а реальную систему, состояния которой S суть результаты опытных данных. При таком подходе тоже можно говорить о законе движения, понимая его в вероятностном смысле, т. е. как условную вероятность состояния S2
в момент t2 при условии, что в момент t1
система имела состояние S1. Теперь забудем на минуту о законе движения. Обозначим через N полное число возможных состояний подсистемы B
и будем представлять себе дело таким образом, что в любой момент времени подсистема B может с равной вероятностью принять любое из N
состояний независимо от того, какое состояние она имела в предыдущий момент. Попытаемся количественно выразить степень (или силу) причинно-следственного влияния подсистемы A на такую безынерционную и «беззаконную» подсистему B. Пусть B под действием A переходит в некоторое совершенно определенное состояние. Ясно, что «сила влияния», которая требуется для этого от A, зависит от числа N и тем больше, чем больше N. Если, например, N = 2, то система B, даже будучи совершенно не связана с A, под действием каких-то случайных причин может с вероятностью 1/2
перейти в то самое состояние, которое «рекомендует» система A.
Если же N
= 109, то, заметив такое совпадение, мы вряд ли усомнимся во влиянии A на B. Следовательно, мерой «силы влияния» A на B
в данном единичном акте, т. е. по существу мерой интенсивности причинно-следственной связи между двумя событиями — состоянием подсистемы A
в интервале времени от t1 до t2 и состоянием подсистемы B в момент t2 — должна служить какая-то монотонно возрастающая функция N. В кибернетике эта мера называется количеством информации, переданной от A к B между моментами времени t1 и t2, а монотонно возрастающей функцией служит логарифм. Итак, в нашем примере количество информации I, переданное от A к B, равно log N.
Выбор логарифмической функции определяется тем ее свойством, что
log N1
N2 = log N1 + log N2.
Пусть система A действует на систему B, состоящую из двух независимых подсистем B1 и B2 с возможным числом состояний N1 и N2 соответственно (рис. 1.3). Тогда число состояний системы B есть N1×N2, а количество информации I, которое надо передать системе B, чтобы она приняла одно определенное состояние, есть благодаря указанному свойству логарифма сумма
I = log N1 N2 = log N1
+ log N2 = I1 + I2,
где I1 и I2 — количества информации, потребные подсистемам B1 и B2. Благодаря этому свойству информация принимает определенные черты субстанции, она распределяется по независимым подсистемам подобно жидкости, разливающейся по сосудам. Мы говорим о слиянии и разделении информационных потоков, об информационной емкости, о переработке информации и ее хранении.
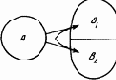
Рис. 1.3. Воздействие на две независимые подсистемы
Вопрос о хранении информации связан с вопросом о законе движения. Выше мы мысленно отключили закон движения, чтобы определить понятие передачи информации. Если мы теперь рассмотрим закон движения с новой точки зрения, то он сводится к передаче информации от системы B в момент времени t1 к той же самой системе B в момент t2. Если состояние системы не меняется с течением времени, то это и есть хранение информации.
Если состояние S2 однозначно определяется состоянием S1 в предыдущий момент времени, то систему называют полностью детерминированной. Если имеет место однозначная зависимость S1 от S2, то систему называют обратимой; для обратимой системы можно, в принципе, по заданному состоянию вычислить все предыдущие состояния, поэтому потери информации не происходит. Если система необратима, информация теряется. Закон движения в сущности есть нечто, регулирующее поток информации во времени от системы к ней самой.
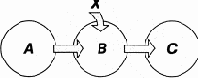
Рис. 1.4. Канал связи
На рис. 1.4 изображена схема передачи информации от системы A к системе C через систему B. Эта последняя носит название канала связи. На состояние B может влиять не только состояние системы A, но еще какой-либо не поддающийся контролю фактор X, называемый помехой. Конечное состояние системы C в этом случае зависит не только от состояния A, но и от фактора Х (искажение информации). Еще одна важная схема обмена информации изображена на рис. 1.5. Это так называемая схема обратной связи. Состояние системы A в момент времени t1 влияет на состояние B в момент времени t2, а это последнее влияет на состояние системы A в момент времени t3. Путь информации замыкается.
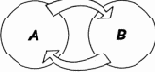
Рис. 1.5. Обратная связь
На этом мы пока ограничим наше знакомство с общими понятиями кибернетики и вернемся к эволюции жизни на Земле.