Математический анализ в Maple
с контурными линиями
Шаг 1
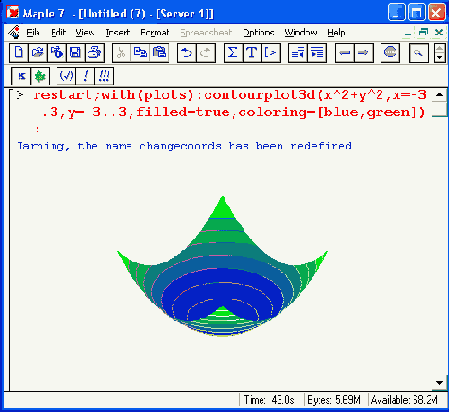
Рисунок 12.9. График поверхности с контурными линиями
Шаг 1
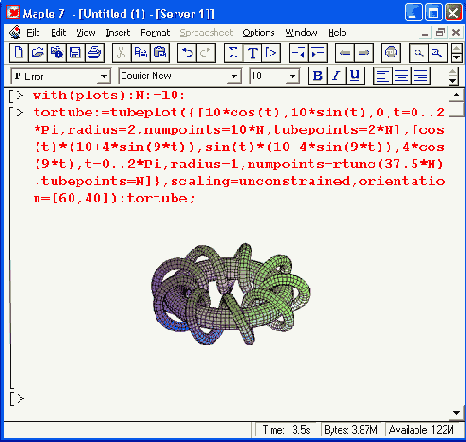
Рисунок 12.10. Тор с обмоткой — толстой спиралью
Шаг 1
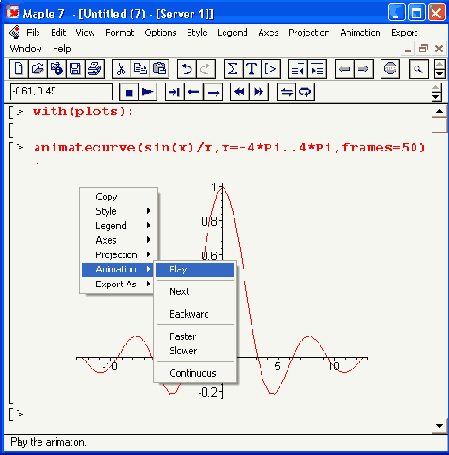
Рисунок 12.15. Пример анимационного построения графика функцией animatecurve
Шаг 1
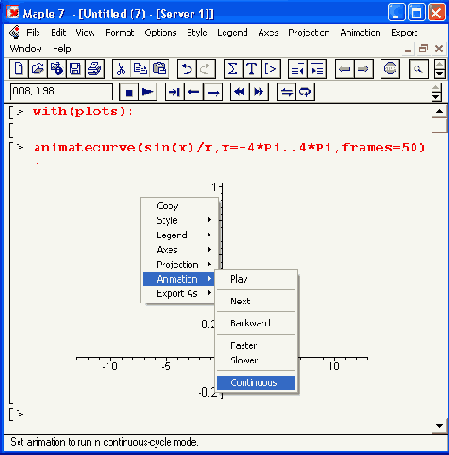
Рисунок 12.16. Анимация функции sin(i*x)/(i*x) на фоне неподвижной синусоиды
В документе Рисунок 12.16 строятся две функции — не создающая анимации функция sin(x) и создающая анимацию функция sin(i*x)/(i*x), причем в качестве переменной t задана переменная i. Именно ее изменение и создает эффект анимации. Проигрыватель анимационных клипов и меню, описанные выше, могут использоваться для управления и этим видом анимации. Обратите внимание на вызов графических функций в этом примере командой with и на синтаксис записи этих функций.
К сожалению, картинки в книгах всегда неподвижны и воспроизвести эффект анимации невозможно. Можно лишь представить несколько текущих кадров анимации. Представленная на Рисунок 12.16 картина соответствует последнему кадру анимации.
Еще один пример анимации представлен на Рисунок 12.17. Этот документ показывает кадр анимированного процесса улучшения приближения синусоидальной функции рядом с различным числом членов (и порядком последнего члена ряда). Результирующая картина, изображенная на Рисунок 12.17, показывает как приближаемую синусоидальную функцию, так и графики всех рядов, которые последовательно выводятся в ходе анимации.
Шаг 1
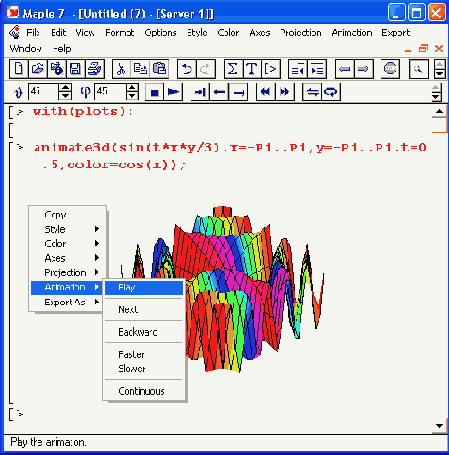
Рисунок 12.18. Подготовка трехмерного анимационного графика
На Рисунок 12. 18 показано также контекстное меню поля выделенного графика. Нетрудно заметить, что с помощью этого меню (и содержащихся в нем подменю) можно получить доступ к параметрам трехмерной графики и выполнить необходимые операции форматирования, такие как включение цветовой окраски, выбор ориентации фигуры и т. д.
Назначение параметров, как и средств управления проигрывателем анимационных клипов, было описано выше.
Шаг 1
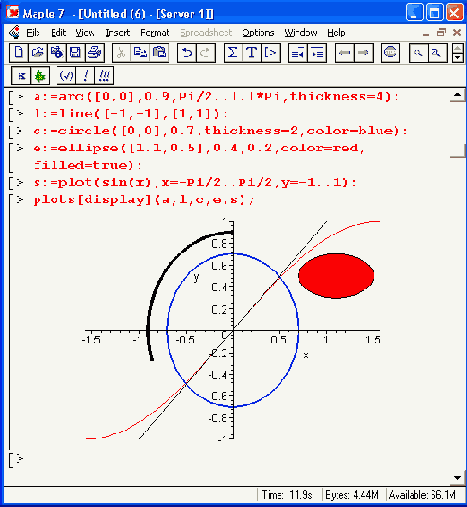
Рисунок 12.19. Примеры применения примитивов двумерной графики пакета plottools
Рисунок 12.20 иллюстрирует построение средствами пакета plottools четырех разноцветных стрелок, направленных в разные стороны. Цвет стрелок задан списком цветов с, определенным после команды загрузки пакета. Для построения стрелок используется примитив arrow с соответствующими параметрами.
Шаг 1
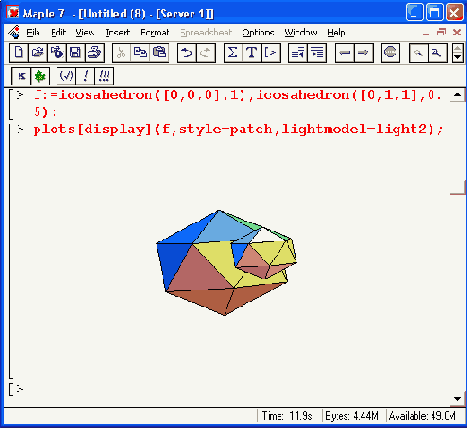
Рисунок 12.22. Построение цилиндра и двух граненых шаров
Шаг 1
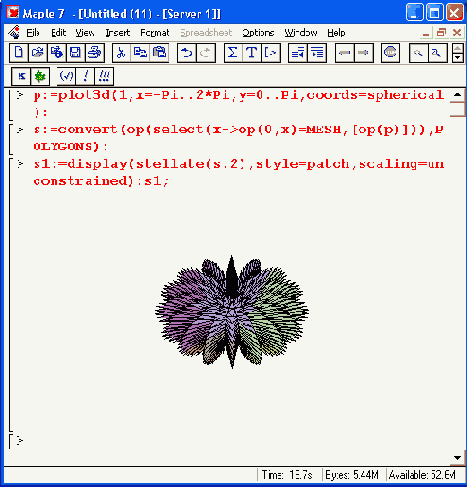
Рисунок 12.25. Построение трехмерной фигуры — «шкурки ежа»
Шаг 1
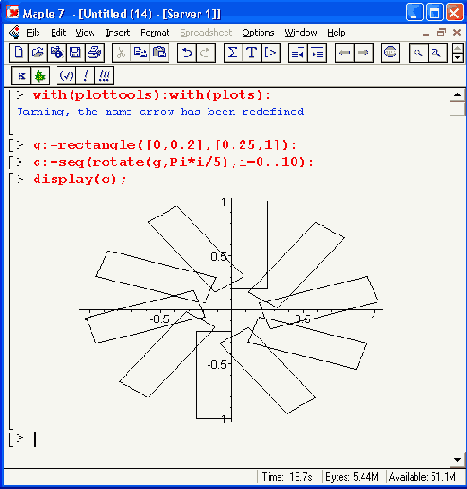
Рисунок 12.28. Построение фигуры, образованной вращением прямоугольника
Шаг 1
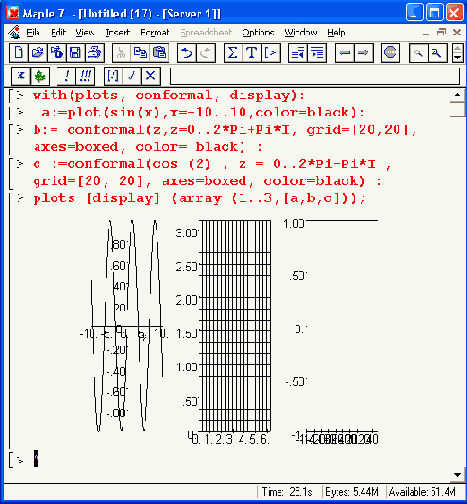
Рисунок 12.31. Пример расположения трех графиков в строке вывода по горизонтали
Шаг 1
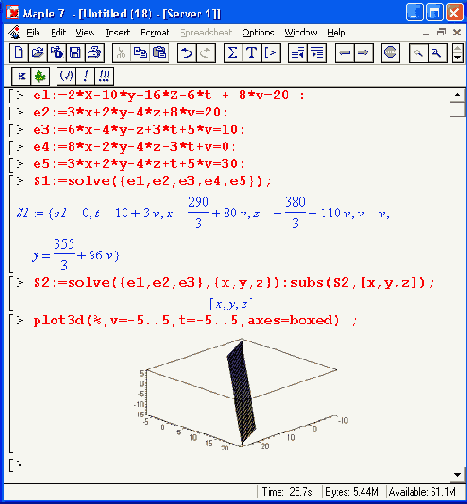
Рисунок 12.32. График, представляющий решения системы линейных уравнений
На Рисунок 12.32 система задана пятью равенствами: el, е2, еЗ, е4 и е5. Затем функцией solve получено вначале решение для всех переменных (для иллюстрации), а затем для трех переменных х, у и z. Для получения решения в виде списка, а не множества, как в первом случае для всех переменных, использована функция подстановки subs. После этого функция plot3d строит плоскость решения в пространстве.
Шаг 1
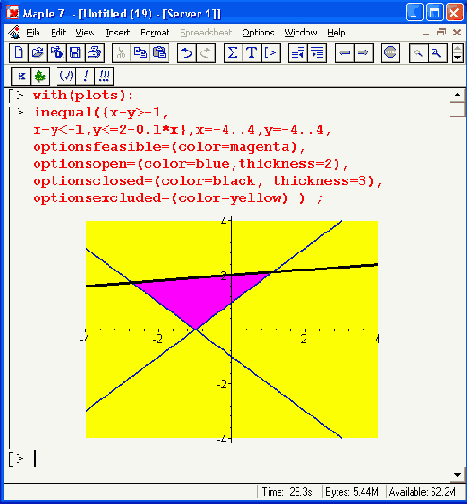
Рисунок 12.33. Пример графической интерпретации решения системы неравенств
Обратите внимание на задание цветов: optionsfeasible задает цвет внутренней области, для которой удовлетворяются все неравенства (равенства), optionsopen и optionsdosed задают цвета открытых и закрытых границ областей графика, optionsexcluded используется для цвета внешних областей. График дает весьма наглядную интерпретацию действия ряда неравенств (или равенств).
Шаг 1
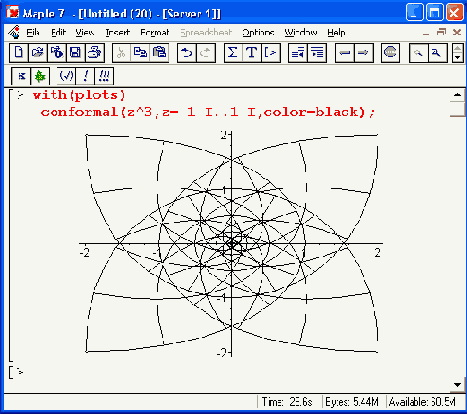
Шаг 1
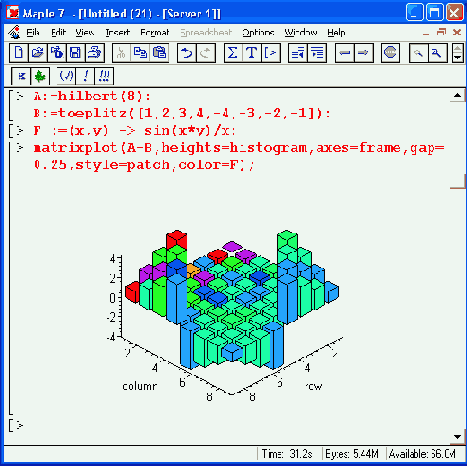
Рисунок 12. 35. Графическое представление матрицы
На Рисунок 12.35 показана графическая визуализация матрицы, полученной как разность матриц А и В. Для усиления эффекта восприятия применяется функциональная закраска разными цветами. Для задания цвета введена процедура F.
Шаг 1
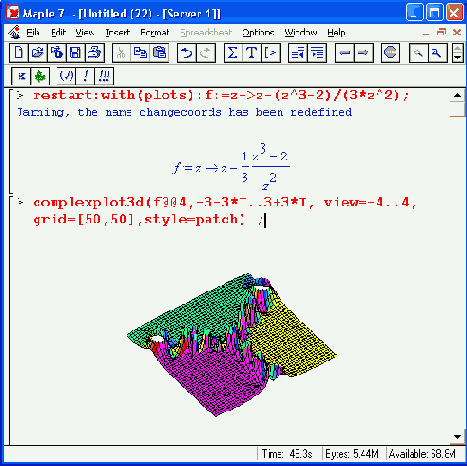
Рисунок 12.36. Наблюдение за процессом ньютоновских итераций в трехмерном пространстве
ВНИМАНИЕ
Риск работы с этим примером заключается в том, что в системе Maple 7 он иногда вызывает фатальные ошибки, ведущие к прекращению работы с системой. Обычно при запуске этого примера сразу после загрузки системы Maple такого не происходит, но, когда память загружена, сбой вполне возможен. Объективности ради надо заметить, что в системах Maple 6 и 7 подобное поведение системы не было замечено. Тем не менее рекомендуется записывать подобные примеры на диск перед их запуском.
Шаг 1
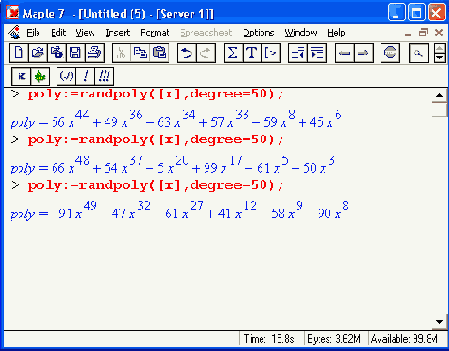
> with(plots):
complexplot(SA.x=-1.2..1.2.style=point):
построить комплексные корни полученного случайного полинома в виде точек • на комплексной плоскости. Один из таких графиков (их можно построить множество) показан на Рисунок 12.37.
Шаг 1
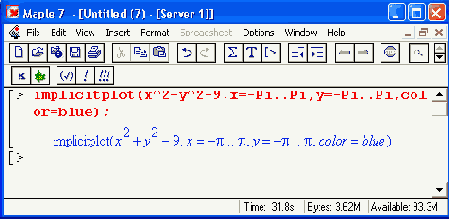
Рисунок 12.1. Графики, построенные с помощью функций polarptot и impticitplot
Шаг 1
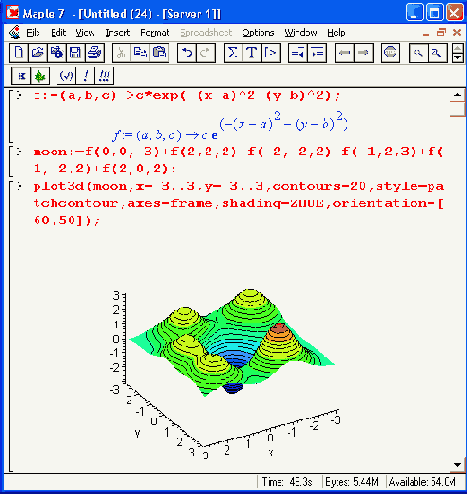
Рисунок 12.38. Построение графика поверхности с множеством экстремумов
Наглядность этого графика усилена за счет применения функциональной окраски и контурных линий, нанесенных на саму поверхность. Все эти возможности обеспечивают параметры основной функции plot3d.
А на Рисунок 12.39 представлен еще один способ задания поверхности — с помощью функции двух угловых переменных f(theta, phi).
При построении этого рисунка также используются функциональная окраска и построение контурных линий.
Шаг 1
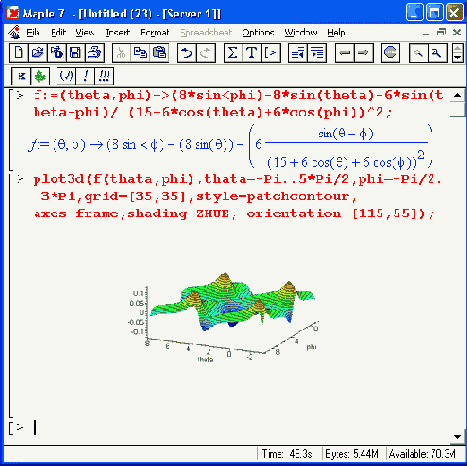
Рисунок 12.39. Построение графика поверхности, заданной функцией двух угловых переменных
Шаг 1
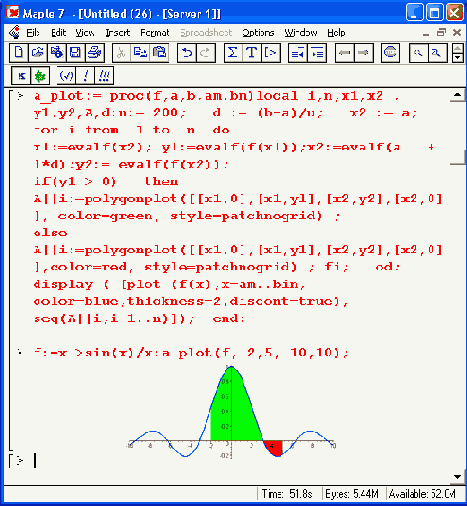
Рисунок 12.41. Графическое представление определенного интеграла
Шаг 1
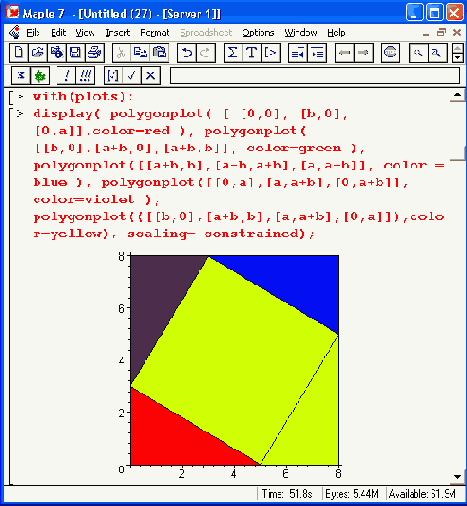
Рисунок 12.42. Графическая иллюстрация к теореме Пифагора
Шаг 1
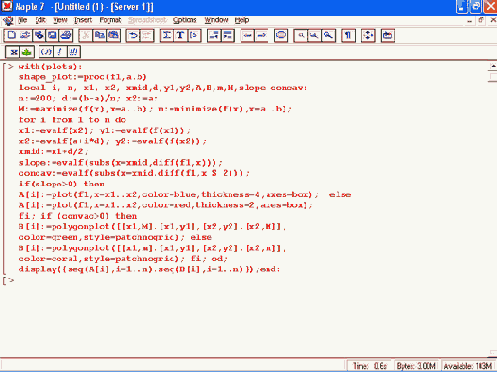
Шаг 1
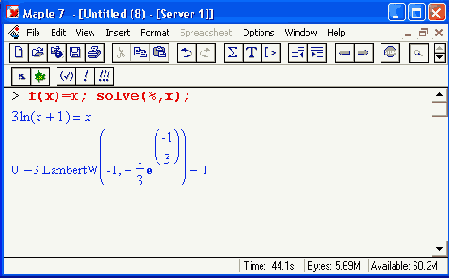
> evalf(%);
0., 5.711441084
Однако как сделать процесс решения достаточно наглядным? Обычно для этого строят графики двух зависимостей — прямой х и кривой f(x) — и наносят на них ступенчатую линию перемещения точки xk. Специальной функции для графиков подобного рода Maple 7 не имеет. Однако можно составить специальную процедуру для их построения .Ее листинг, заимствованный из примера, описанного в пакете обучения системе Maple 7 - PowerTools, представлен ниже:
Шаг 1
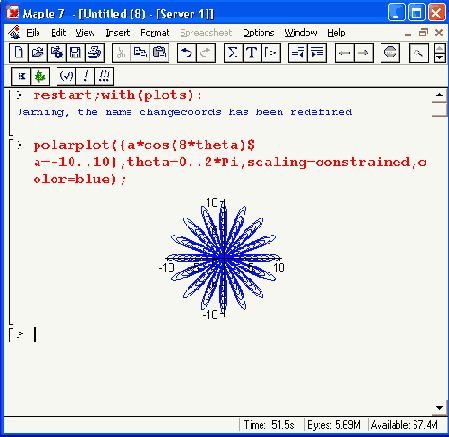
Рисунок 12.46. Семейство кардиоид на одном графике
Еще одно семейство кардиоид, на сей раз шестилепестковых, представлено на Рисунок 12.47. Здесь также изменяемым параметром каждой фигуры является ее размер, заданный параметром а.
Фигуре, представленной на Рисунок 12.48, трудно дать определенное название. Назовем ее волнообразной спиралью.
По образу и подобию приведенных фигур читатель может опробовать свои силы в создании новых красочных фигур в полярной системе координат. Некоторые из них поразительно напоминают снежинки, картинки в калейдоскопе и изображения морских звезд. Если убрать параметр color=black, .введенный ради черно-белой печати картинок в книге, то можно усилить красочность фигур за счет их разноцветной окраски.
Шаг 1
Шаг 1
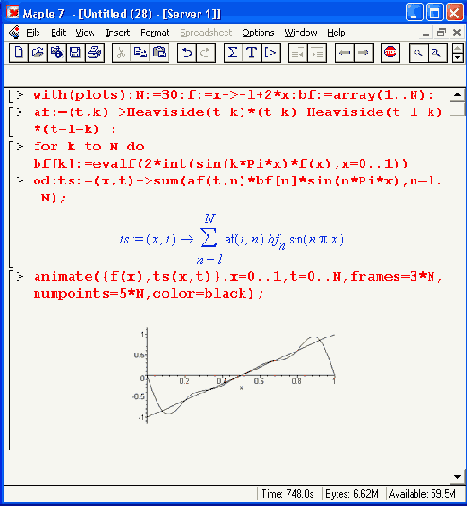
Рисунок 12.50. Один из первых стоп-кадров анимации разложения импульса в ряд Фурье
Рисунок 12.51 показывает завершающий стоп- кадр анимации, когда число гармоник N равно 30. Нетрудно заметить, что такое число гармоник в целом неплохо описывает большую часть импульса, хотя в. его начале и в конце все еще заметны сильные отклонения.
Для f(x) = 1 строится приближение для однополярного импульса с длительностью 1 и амплитудой 1, при f(x) =х — приближение для пилообразного линейно нарастающего импульса, при f(x) =х^2 — приближение для нарастающего по параболе импульса, при f(x)=signum(x-l/2) — приближение для симметричного прямоугольного импульса-меандра и т. д. Фактически можно наблюдать анимационную картину изменения формы импульса по мере увеличения числа используемых для синтеза гармоник. Выбор используемого числа гармоник осуществляет амплитудный селектор — функция a= f(t,k), основанная на применении функции Хевисайда.
Шаг 1
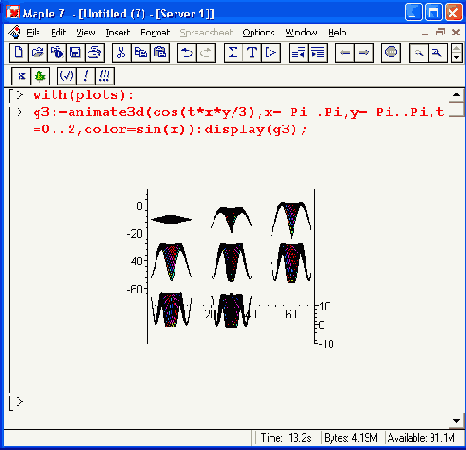
Рисунок 12.53. Фазы анимации трехмерной поверхности
Применение анимации дает повышенную степень визуализации решений ряда задач, связанных с построением двумерных и трехмерных графиков. Следует отметить, что построение анимированных графиков требует дополнительных и достаточно существенных затрат оперативной памяти. Поэтому злоупотреблять числом стоп-кадров таких графиков не стоит.
Шаг 1
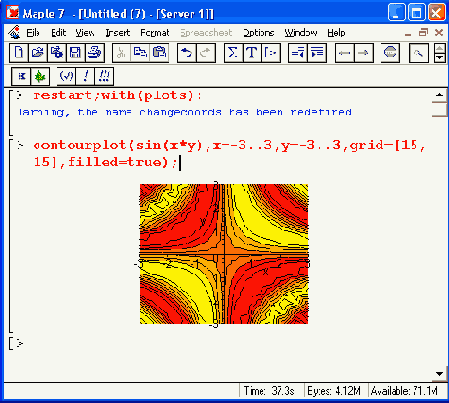
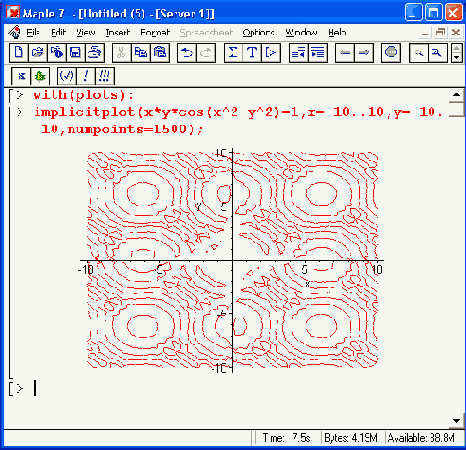
Рисунок 12.2. Пример построения графика функции линиями равного уровня
Обратите внимание на то, что данная функция по умолчанию строит легенду — она видна под графиком в виде линий с надписями. К сожалению, в данном варианте окраски сами контурные линии получаются черными и их невозможно отличить. Однако если убрать параметр filled=true, то контурные линии (и линии легенды) будут иметь разный цвет и легко различаться.
Функция contourplot позволяет строить и графики ряда функций. Пример такого построения показан на Рисунок 12.3. Множество окружностей на этом рисунке создается четырьмя поверхностями, заданными функциями cl, с2, сЗ и с4.
Шаг 1
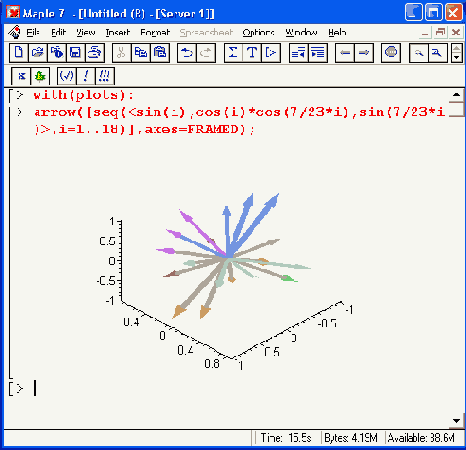
Рисунок 12.54. Построение стрелок с помощью функции arrow
Шаг 1
Шаг 1
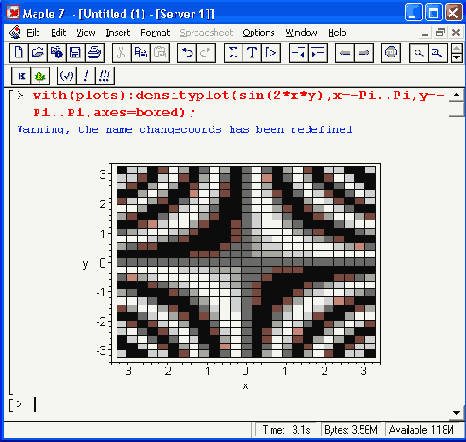
Рисунок 12.4. Графики плотности и поля векторов
Обычно графики такого типа не очень выразительны, но имеют свои области применения. К примеру, оттенки окраски полупрозрачной жидкости могут указывать на рельеф поверхности дна емкости, в которой находится эта жидкость.
Шаг 1
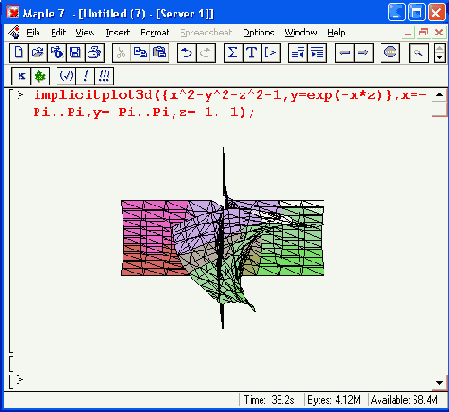
Рисунок 12.5. Примеры применения функции implidtplot3d
На Рисунок 12. 6 показана одна из таких фигур. Она поразительно напоминает раковину улитки. Функциональная окраска достигнута доработкой графика с помощью панели форматирования.
Эта функция может использоваться и для построения ряда трубчатых объектов в пространстве. При этом автоматически задается алгоритм удаления невидимых линий даже для достаточно сложных фигур. Это наглядно иллюстрирует пример на Рисунок 12.7, показывающий фигуру «цепи». Не правда ли, реалистичность этой фигуры поражает воображение?
Можно долго размышлять о том, как те или иные математические закономерности описывают предметы реального мира, положенные в основу тех или иных геометрических объектов, или, возможно, о гениальности людей, сумевших найти такие закономерности для многих из таких объектов. В наше время Maple 7 открывает огромные возможности для таких людей.
Шаг 1
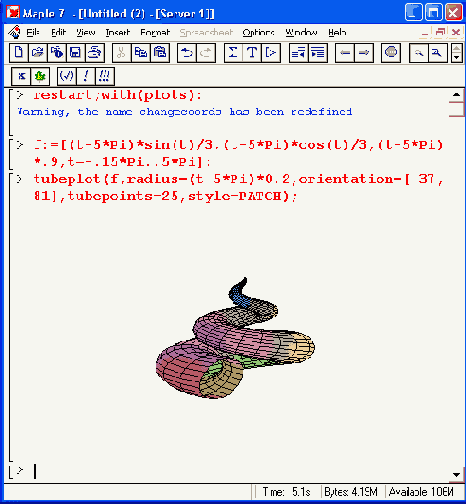
Рисунок 12.6. Построение графика- «улитки»
Шаг 2
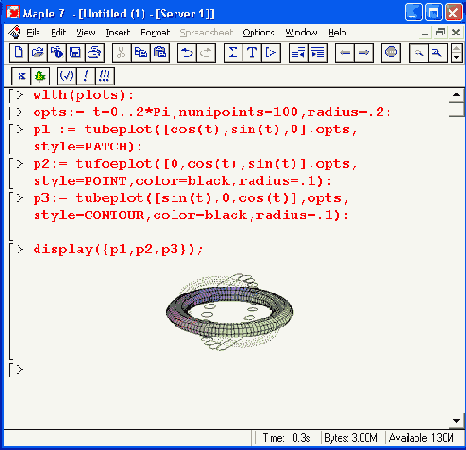
Рисунок 12.11. Три пересекающихся тора с разными стилями построения
Наконец, на Рисунок 12.12 показано построение тора с тонкой обмоткой. Рекомендуется внимательно посмотреть на запись функции tubeplot в этом примере и в примере, показанном на Рисунок 12.11. Можно также поэкспериментировать с управляющими параметрами графика, от которых сильно зависят его представительность и наглядность.
Шаг 2
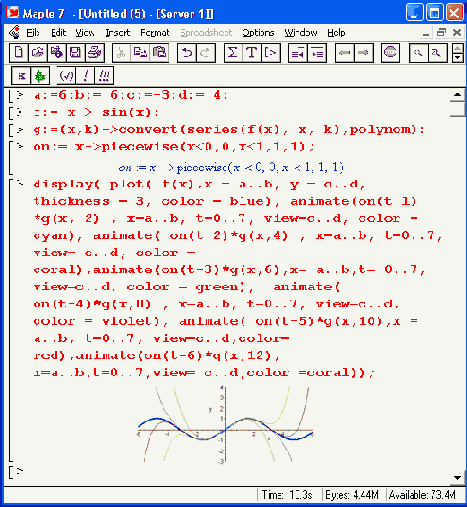
Рисунок 12.17. Анимационная демонстрация приближения синусоиды рядом с меняющимся числом членов
Анимация графиков может найти самое широкое применение при создании учебных материалов. С ее помощью можно акцентировать внимание на отдельных параметрах графиков и образующих их функций и наглядно иллюстрировать характер их изменений.
Шаг 2
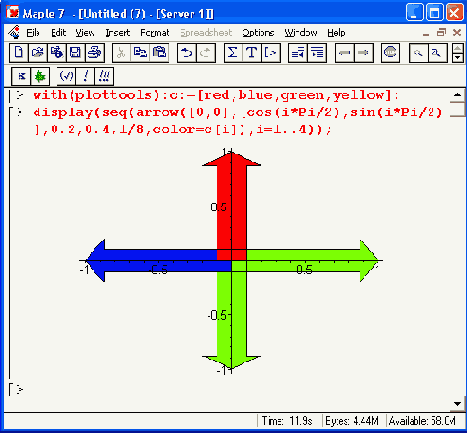
Рисунок 12.20. Построение разноцветных стрелок, направленных в разные стороны
Примитивы могут использоваться в составе графических процедур, что позволяет конструировать практически любые типы сложных графических объектов. В качестве примера на Рисунок 12.21 представлена процедура SmithChart, которая строит хорошо известную электрикам диаграмму Смита (впрочем, несколько упрощенную). В этой процедуре используется примитив построения дуг arc. При этом задается верхняя часть диаграммы, а нижняя получается ее зеркальным отражением.
Примечание 1
Примечание 1
Обратите внимание на то, что, начиная с Рисунок 12.21, мы не указываем загрузку паета plottools, поскольку она уже была проведена ранее. Однако надо помнить, что все примеры этого раздела предполагают, что такая загрузка обеспечена. Если вы использовали команду restart или только что загрузили систему Maple 7, то для исполнения примера Рисунок 12.21 и последующих примеров надо исполнить команду with(plottools).
Шаг 2
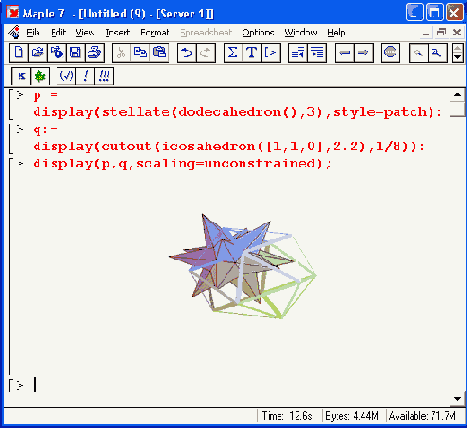
Рисунок 12.23. Построение двух объемных фигур
Шаг 2
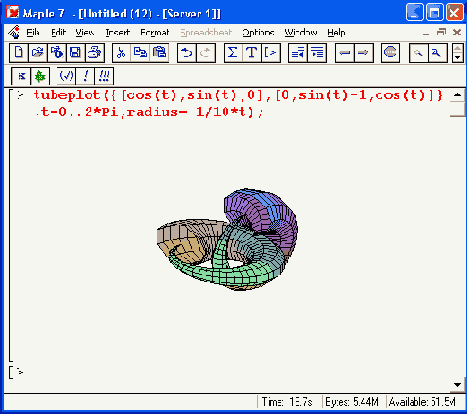
Рисунок 12.26. Построение фигуры «улитка»
Шаг 2
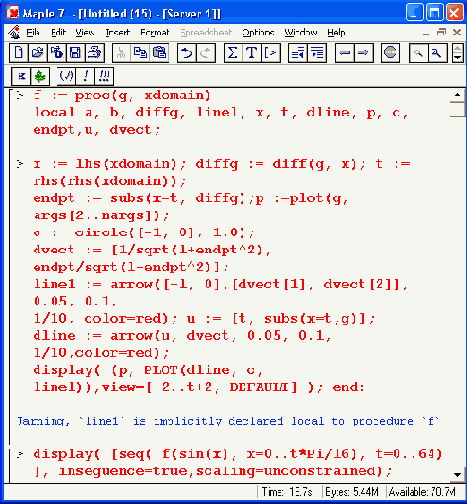
Рисунок 12.29. Пример анимации двумерной графики
Шаг 2
Шаг 2
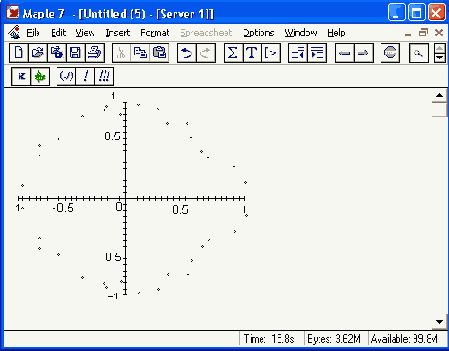
Рисунок 12.37. Расположение корней случайного полинома на комплексной плоскости
Можно заметить любопытную закономерность — точки, представляющие корни случайного полинома, укладываются вблизи окружности единичного радиуса с центром в начале координат. Однако этот пример, приводимый в ряде книг по Maple, показывает, что порою вычисления могут давать довольно неожиданные результаты. Кстати говоря, аналитически можно вычислять корни полинома с максимальной степенью не более четырех.
Шаг 2
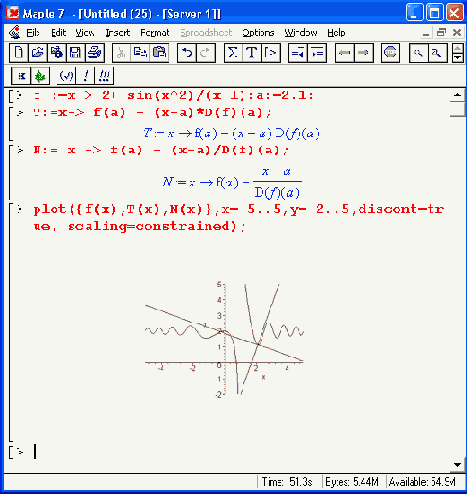
Рисунок 12.40. Построение касательной и перпендикуляра к заданной точке графика функции f(x)
Шаг 2
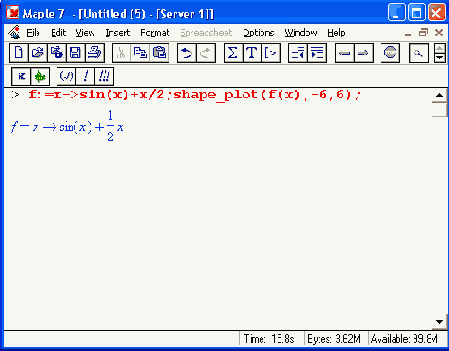
Рисунок 12.43 дает наглядное представление о поведении заданной функции. Рекомендуется опробовать данную процедуру на других функциях. Следует отметить, что, поскольку процедура использует функции ntiroimize и maximize, она может давать сбои при исследовании сложных функций, содержащих специальные математические функции или особенности. Иногда можно избежать такой ситуации, исключив особенность. Например, для анализа функции sin(x)/x можно записать ее в виде:
>f:=x->if x=0 then 1 else sin(x)/x
end if;
shape_plot(f(x),-10,10);
Исполнение приведенной выше строки ввода дает график, представленный на Рисунок 12.44.
Шаг 2
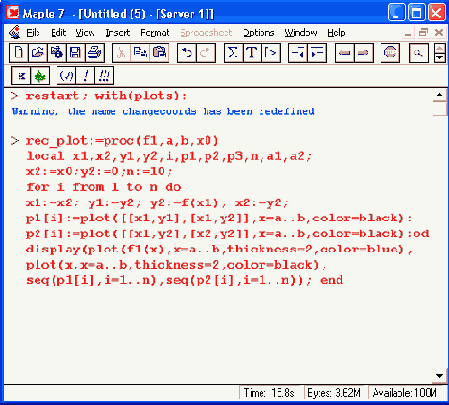
>rec_p1ot( f(x), 0, 8, х0):
можно наблюдать график, иллюстрирующий итерационный процесс. Он представлен на Рисунок 12.45.
Шаг 2
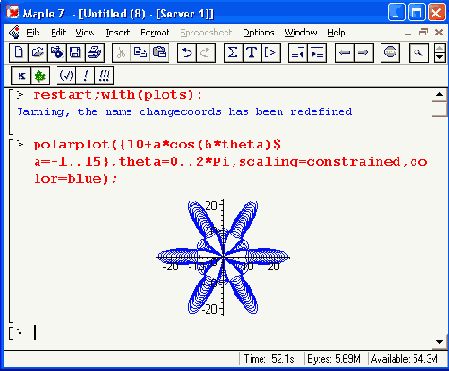
Рисунок 12.47. Семейство шестилепестковых кардиоид
Шаг 2
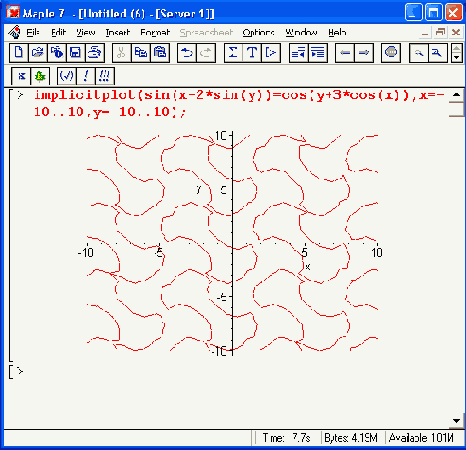
Рисунок 12.49. Построение сложных фигур, заданных импликативными функциями
Шаг 2
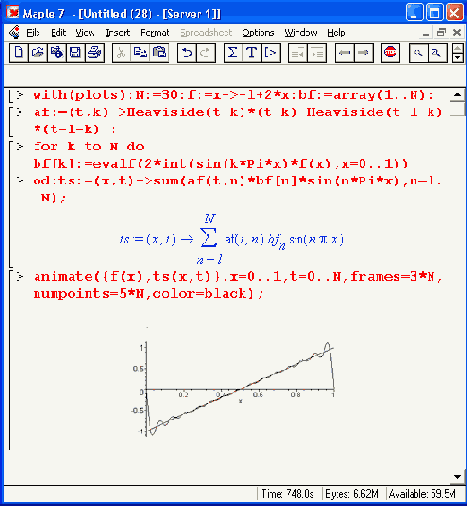
Рисунок 12.51. Второй (завершающий) кадр анимации
Самым интересным в этом примере оказывается наблюдение за зарождением и эволюцией эффекта Гиббса — так называют волнообразные колебания на вершине импульса, связанные с ограничением числа гармоник при синтезе сигнала. С ростом числа гармоник эффект Гиббса не исчезает, просто обусловленные им выбросы вблизи разрывов импульса становятся более кратковременными. Амплитуда импульсов может достигать 18% от амплитуды перепадов сигнала, что сильно ухудшает приближение импульсных сигналов рядами Фурье и вынуждает математиков разрабатывать особые меры по уменьшению эффекта Гиббса.
Можно ли наблюдать одновременно все фазы анимации? Можно! Для этого достаточно оформить анимационную картину, созданную функцией animate, в виде отдельного графического, объекта например g, после чего можно вывести все его фазы оператором display. Это и иллюстрирует Рисунок 12.52. На этот раз задано f(x) = signum(x-l/2) и N = 25. Таким образом рассматриваются симметричные прямоугольные импульсы - меандр. У каждого рисунка координатные оси с делениями удалены параметром axes=none.
Шаг 2
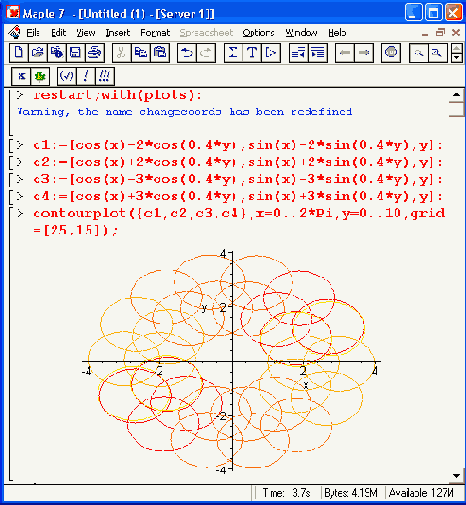
Рисунок 12.3. Пример построения графиков многих функций линиями равного уровня
ВНИМАНИЕ
Обратите внимание, что на многих графиках Maple 7 по умолчанию вписывает легенду,то есть список линий с обозначениями. Иногда (как, например, на Рисунок 12.3) этот список оказывается просто некстати. Легенду можно убрать, расширив заодно место для графика, сняв флажок Show Legend в меню Legend, которое появляется при двойном щелчке на графике (это меню видно на Рисунок 12.3). То же самое можно сделать с помощью той же команды в контекстном меню. Заодно запомните, что легенду можно редактировать, выполнив команду Edit Legend.
Следует отметить, что хотя графики в виде линий равного уровня выглядят не так эстетично и естественно, как обычные графики трехмерных поверхностей (ибо требуют осмысления результатов), у них есть один существенный плюс - экстремумы функций на таких графиках выявляются порой более четко, чем на обычных графиках. Например, небольшая возвышенность или впадина за большой «горой» на обычном графике может оказаться невидимой, поскольку заслоняется «горой». На графике линий равного уровня этого эффекта нет. Однако выразительность таких графиков сильно зависит от числа контурных линий.
Шаг 2
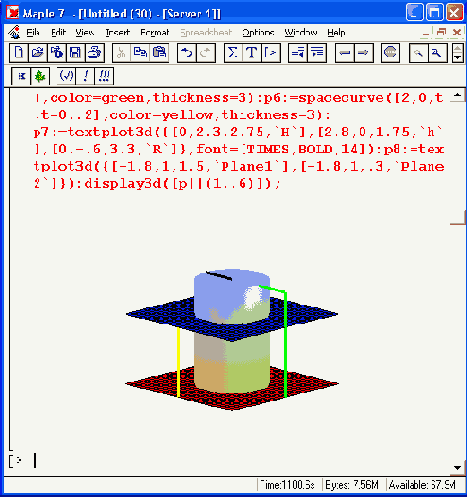
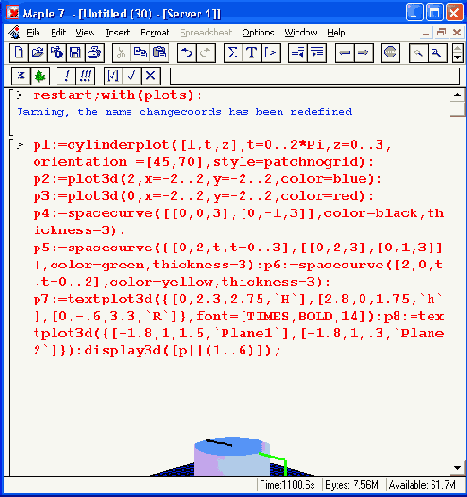
Рисунок 12.55. Пример построения сложного объекта, состоящего из 8 графических и текстовых объектов
Представленный на Рисунок 12.55 объект задает построение восьми графических объектов от р! до р8. Среди них цилиндр, две пересекающие его плоскости и иные (в том числе текстовые) объекты. Обратите внимание на способ вывода этих объектов функцией display3d. Этот пример показывает, что с помощью графических программных средств Maple 7 можно строить достаточно замысловатые графики, которые могут использоваться для визуализации тех или иных геометрических и иных объектов.
Шаг 2
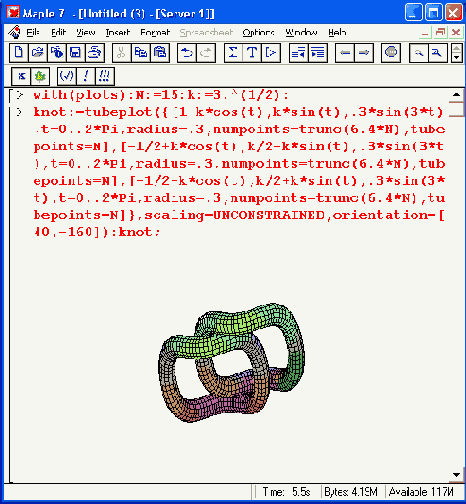
Рисунок 12.7. Фигура «цепи», построенная с применением функции tubeplot
Шаг 3
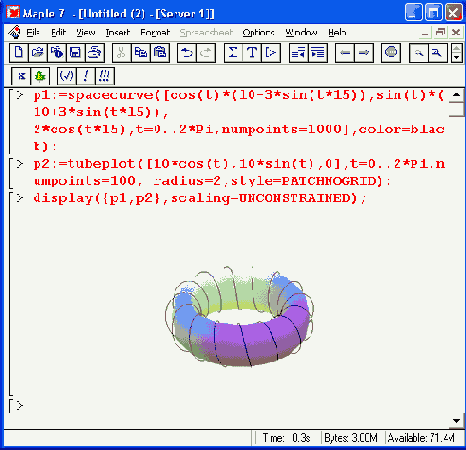
Рисунок 12.12. Тор с тонкой обмоткой
В ряде случаев наглядно представленные фигуры можно строить путем объединения однотипных фигур. Пример графика подобного рода представлен на Рисунок 12.13. Здесь готовится список графических объектов s, смещенных по вертикали. С помощью функции display они воспроизводятся на одном графике, что повышает реалистичность изображения.
Последний пример имеет еще одну важную особенность — он иллюстрирует задание графической процедуры, в теле которой используются функции пакета plots. Параметр п этой процедуры задает число элементарных фигур, из которых строится полная фигура. Таким образом, высотой фигуры (или шириной «шины») можно управлять. Возможность задания практически любых графических процедур средствами Maple-языка существенно расширяет возможности Maple.
Наглядность таких графиков, как графики плотности и векторных полей может быть улучшена их совместным применением. Такой пример показан на Рисунок 12.14.
Шаг 3
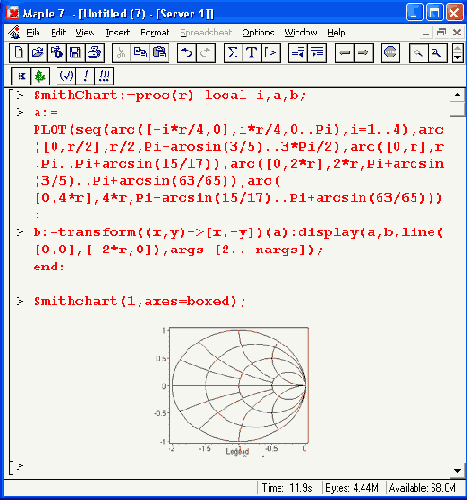
Рисунок 12.21. Построение диаграммы Смита
Шаг 3
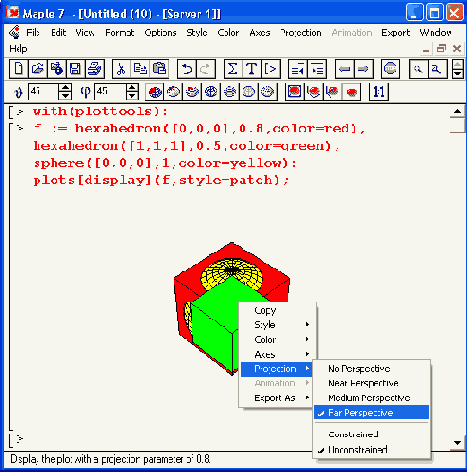
Рисунок 12.24. Примеры применения примитивов трехмерной графики пакета plottools
Построение еще одной забавной трехмерной фигуры — «шкурки ежа» — демонстрирует Рисунок 12.25. В основе построения лежит техника создания полигонов. Построение фигур, очень напоминающих улитки, показано на Рисунок 12.26. При построении этих фигур используется функция tubeplot. Обратите внимание на то, что строятся две входящие друг в друга «улитки».
Наконец, на Рисунок 12.27 показано построение фигуры — бутылки Клейна. Фигура задана рядом своих фрагментов, определенных в процедуре cleinpoints. Эта процедура является еще одним наглядным примером программирования графических построений с помощью Maple-языка.
С другими возможностями этого пакета читатель теперь справится самостоятельно или с помощью данных справочной системы. Много примеров построения сложных и красочных фигур с применением пакета plottools можно найти в Интернете на сайте фирмы Maple Software, в свободно распространяемой библиотеке пользователей системы Maple и в книгах по этой системе.
Шаг 3
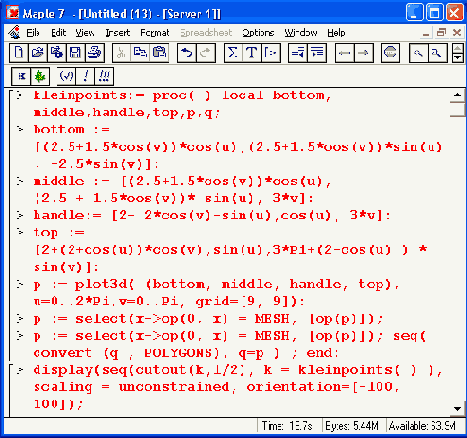
Рисунок 12.27. Построение фигуры «бутылка Клейна»
В этом примере полезно обратить внимание еще и на функцию поворота фигуры — rotate. Именно сочетание этих двух функций (мультиплицирования и поворота базовой фигуры — прямоугольника) позволяет получить сложную фигуру, показанную на Рисунок 12.28.
Шаг 3
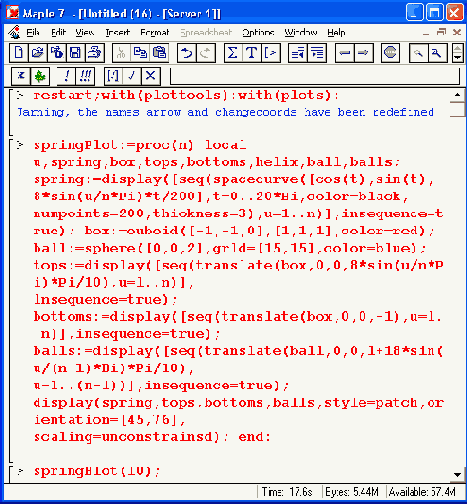
Рисунок 12.30. Имитация отстрела шара сжатой упругой системой
Управление анимацией, реализованной средствами пакета plottools, подобно уже описанному ранее. Последний пример также прекрасно иллюстрирует возможности применения Maple 7 при математическом моделировании различных явлений, устройств и систем.
Шаг 3
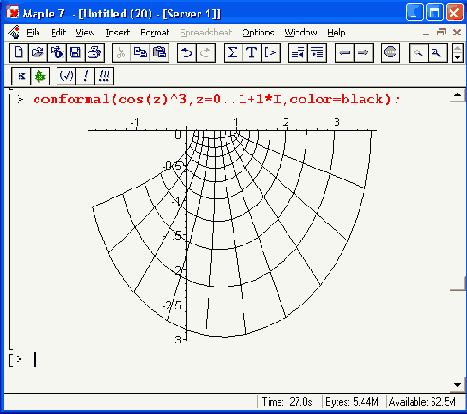
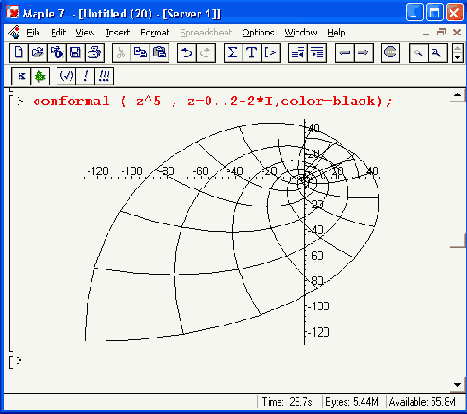
Рисунок 12.34. Конформное отображение на комплексной плоскости графиков трех зависимостей
Средства конформного отображения в Maple 7, к сожалению, остаются рудиментарными и вряд ли достаточными для специалистов в этой области математики.
Шаг 3
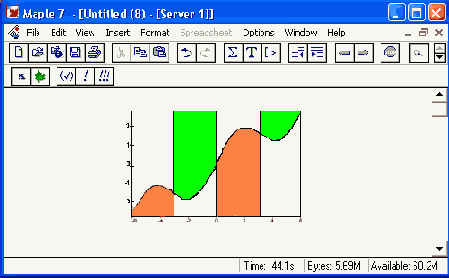
Рисунок 12.43. Визуализация поведения функции f(х)
Шаг 3
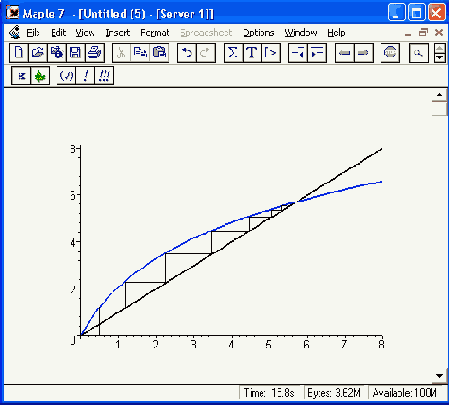
Рисунок 12.45. Иллюстрация процесса итераций
Нетрудно заметить, что для данной функции процесс итераций хотя и не очень быстро, но уверенно сходится к точке пересечения прямой у = х и кривой y=f(x). Вы можете, меняя зависимость f(x), провести исследования сходимости уравнений х = f(x).
Шаг 3
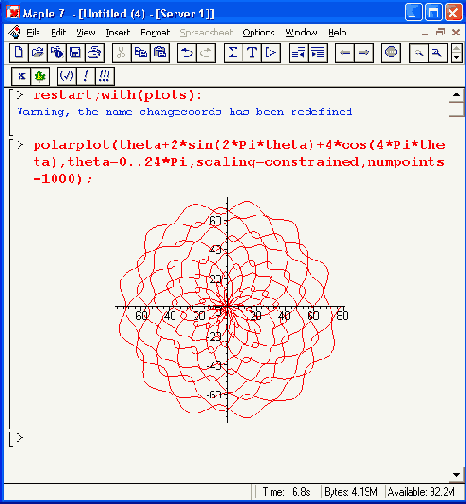
Рисунок 12.48. Фигура— волнообразная спираль
Шаг 3
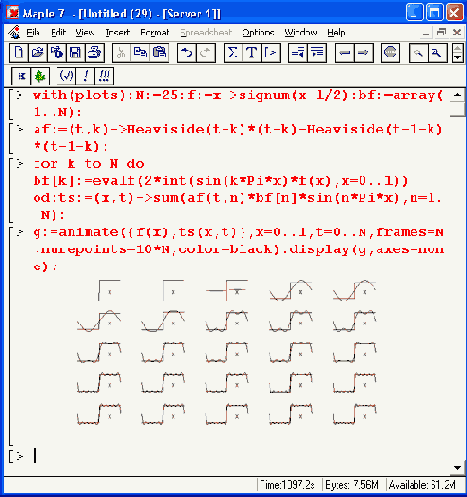
Рисунок 12.52. Иллюстрация получения всех кадров анимации двумерного графика
Любопытно отметить, что при определенных числах гармоник связанная с колебательными процессами неравномерность вершины импульса резко уменьшается. Наблюдение этого явления и является наиболее интересным и поучительным при просмотре данного примера.
При внимательном просмотре Рисунок 12.52 заметно, что после некоторого периода установления фазы анимационной картинки практически повторяются. Это связано с известным обстоятельством — установившийся спектр меандра содержит только нечетные гармоники. Поэтому, к примеру, вид спектрального разложения при 22 гармониках будет тот же, что и при 21 гармонике, при 24 гармониках тот же, что при 23, и т. д. Однако эта закономерность проявляется только при установившемся (стационарном) спектре.
Шаг 3
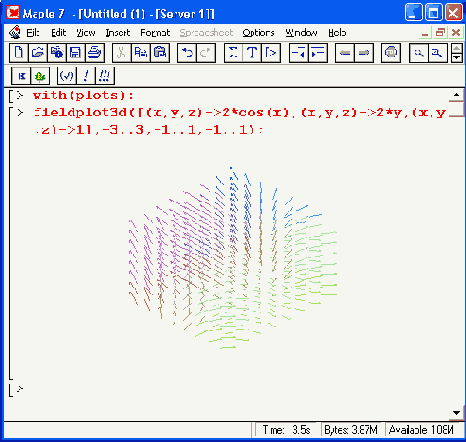
Рисунок 12.8. Построение поля в трехмерном пространстве с помощью векторов
Все сказанное об особенностях таких двумерных графиков остается справедливым и для графиков трехмерных. В частности, для обеспечения достаточной наглядности нужно тщательно отлаживать форматы представления таких графиков.
Шаг 4
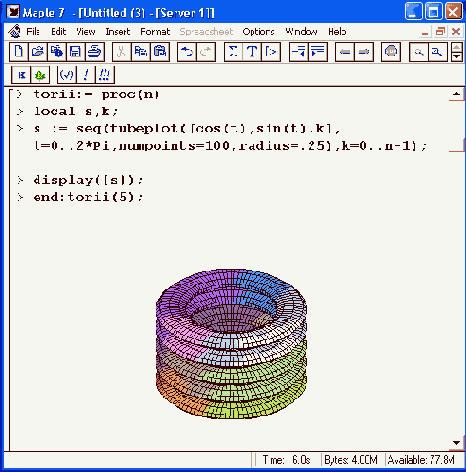
Рисунок 12.13. Построение фигуры, напоминающей шину автомобиля
Шаг 4
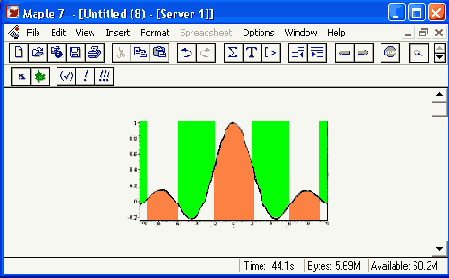
Рисунок 12.44. Визуализация поведения функции sin(x)/x
Данная процедура дает хорошие результаты при анализе функций, представленных полиномами. Вы можете сами убедиться в этом.
Шаг 5
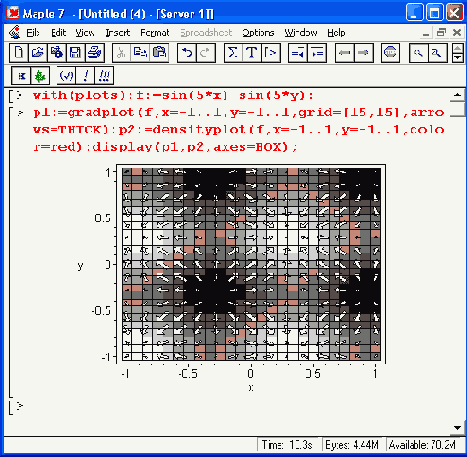
Рисунок 12.14. Пример совместного применения графиков плотности и векторного поля
Этот пример иллюстрирует использование «жирных*- стрелок .для обозначения векторного поля. Наглядность графика повышается благодаря наложению стрелок на график плотности, который лучше, чем собственно стрелки, дает представление о плавности изменения высоты поверхности, заданной функцией.